V I C B e e C o n s u l t i n g

HOME | CASE STUDIES | PEOPLE | REST APIS | CONTACT |

LARGE SCALE PORTFOLIOS | EFFICIENT FRONTIER | RETURN MODELS | RISK AND VARIANCE |

Risk and Variance

Having looked at how to estimate meaningful asset returns, we now turn our attention to variance. Variance is perhaps the simpler and by far the most used measure of risk in portfolio optimization. Yet, whereas most people have a good intuitive understanding of variance when speaking of isolated random events, sometimes that does not translate to multiple events, which is the case when working with a portfolio of assets, or what are the implications of attempting to minimize variance. We provide an elementary overview of portfolio variance in section Variance and Correlation below.

The Models API

The Models API produces custom factor models given:

The list of portfolio and market assets can contain most global publicly traded equities, ETFs, and most popular cryptocurrencies. Models spanning multiple overlapping historical date range are calculated efficiently by querying prices only once. Return and covariance are estimated using daily closing prices using the methodology described in the case study Return Models and in the section below. The return and covariance are then adjusted to reflect the provided investment horizon.

A custom model is build in response to each query, reflecting the universe of portfolio and market assets provided. In the rest of this note we provide background material on some of the underlying concepts behind the type of return and variance models calculated by the Models API.

Variance and Correlation

Variance, as the name indicates, is a measure of variability. Most people are familiar with the sample statistics formulas: $$ \begin{aligned} \hat{\mu}_x &= \frac{1}{N} \sum_{k = 1}^N x_k, & \hat{\sigma}_x^2 &= \frac{1}{N-1} \sum_{k = 1}^N (x_k - \hat{\mu})^2, \end{aligned} $$ which provide estimates for the mean, \( \mu_x = E \{ x \} \), and the variance, \( \sigma^2_x = E \{ (x - \mu_x)^2 \} \), of the random variable, \( x \), calculated from the samples \( x_k \), \( k = 1, \cdots, n \).

Now let \( x \) and \( y \) be two assets whose returns we model as random variables. Let the mean and variance of each asset return be given by $$ \begin{aligned} E \{ r_x \} &= \mu_x, & E \{ (r_x - \mu_x)^2 \} &= \sigma^2_x, & E \{ r_y \} &= \mu_y, & E \{ (r_y - \mu_y)^2 \} &= \sigma^2_y. \end{aligned} $$ If we consider a simple portfolio valued at \( \pi \) made up of a combination of the assets \( x \) and \( y \), then[1] $$ \begin{aligned} \pi &= x + y, & \theta_x &= \frac{x}{\pi} \geq 0, & \theta_y &= \frac{y}{\pi} \geq 0, & \theta_x + \theta_y &= 1. \end{aligned} $$ Here \( \theta_x \) and \( \theta_y \) are the percentages of each asset in the portfolio, that is the portfolio weights, and the expected return of the portfolio is the familiar $$ \begin{aligned} \mu = E \{ r \} = \theta_x E \{ r_x \} + \theta_y E \{ r_y \} = \theta_x \, \mu_x + \theta_y \, \mu_y = \theta_x \, \mu_x + (1 - \theta_x) \mu_y, \end{aligned} $$ which expresses the fact the expected return of the portfolio is a combination of the expected return of each asset.

The next natural question is “what is the variance of the portfolio?” In order to answer this question we need more information than we presently have. When calculating, $$ \begin{aligned} \sigma^2 = E \{ (r - \mu)^2 \} = \theta_x^2 \sigma^2_x + \theta_y^2 \sigma^2_y + 2 \theta_x^{} \theta_y^{} E \{ (r_x - \mu_x) (r_y - \mu_y)^2 \} \end{aligned} $$ there appears the new quantity $$ E \{ (r_x - \mu_x) (r_y - \mu_y) \} $$ which depends jointly on \( r_x \) and \( r_y \), and is known as the correlation between \( r_x \) and \( r_y \). It is convenient to rewrite the correlation in terms of the coefficient of correlation, \( \rho_{xy} \), and the standard deviations of the individual assets, as in $$ E \{ (r_x - \mu_x) (r_y - \mu_y) \} = \rho_{x y} \, \sigma_x \, \sigma_y, \qquad -1 \leq \rho_{x y} \leq 1. $$ One consequence of \( \rho_{xy} \) being bounded between -1 and 1, is that the variance of the portfolio is never larger than the variance of the individual assets, which follows from $$ \begin{aligned} \sigma^2 \leq \theta_x^2 \sigma^2_x + \theta_y^2 \sigma^2_y + 2 \theta_x^{} \theta_y^{} \sigma_x^{} \sigma_y^{} = (\theta_x \sigma_x + \theta_y \sigma_y)^2 = (\theta_x \sigma_x + (1 - \theta_x) \sigma_y)^2 \leq \max \{ \sigma_x^2, \sigma_y^2 \}. \end{aligned} $$ Yet, the variance of the portfolio can be smaller than the variance of the individual assets! In fact, it will often be smaller. We shall discuss some concrete situations in the next paragraphs.

Uncorrelated assets

When no correlation exists, that is \( \rho_{x y} = 0 \), the variance of the portfolio is $$ \begin{aligned} \sigma^2 = \theta_x^2 \sigma^2_x + \theta_y^2 \sigma^2_y = \theta_x^2 \sigma^2_x + (1 - \theta_x)^2 \sigma^2_y. \end{aligned} $$ Even if the variance of the assets is the same, that is \( \sigma_y = \sigma_x \), in which case $$ \begin{aligned} \sigma^2 = (\theta_x^2 + \theta_y^2) \sigma^2_x = (\theta_x^2 + (1 - \theta_x^{})^2) \sigma^2_x = (2 \theta_x^2 - 2 \theta_x^{} + 1) \sigma^2_x \geq \frac{1}{2} \sigma_x^2, \end{aligned} $$

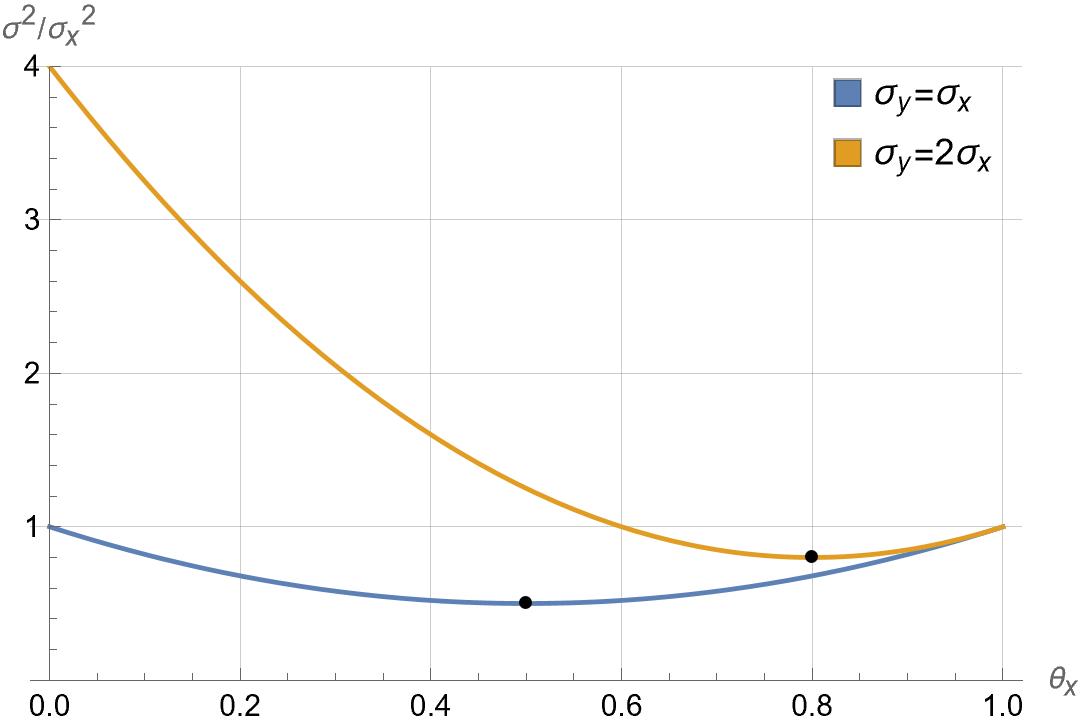
Variance

Fig. 1: Variance

the smallest possible variance is attained by holding the portfolio $$ \begin{aligned} \theta_x &= \theta_y = \frac{1}{2}. \end{aligned} $$ The complete variance, as a function of \( \theta_x \), is shown by the blue curve in the side figure. In this figure, \( \theta_x = 1 \) corresponds to selecting a portfolio with only one asset, \( x \), and \( \theta_x = 0 \) corresponds to selecting a portfolio with only the other asset, \( y \).

Even in the case of more than two assets, if all assets have the same variance, then the portfolio with the minimum variance consists of equal amounts of all assets.

Different asset variances typically skew the combination toward the asset with the least variance, but the portfolio with the minimum possible variance still holds some of the larger variance asset. For example, if \( \sigma_y = 2 \sigma_x \) then $$ \begin{aligned} \sigma^2 = (\theta_x^2 + 4 \theta_y^2) \sigma^2_x = (\theta_x^2 + 4 (1 - \theta_x)^2) \sigma^2_x = (5 \theta_x^2 - 8 \theta_x + 4) \sigma^2_x \geq \frac{4}{5} \sigma_x^2, \end{aligned} $$ which is minimized by the portfolio $$ \begin{aligned} \theta_x &= \frac{4}{5}, & \theta_y = \frac{1}{5}. \end{aligned} $$ This is depicted in Fig. 1 as the orange curve.

On the one hand, it is nice to see that minimizing variance seems to promote diversification, but on the other hand, many are puzzled by the fact that holding an asset with a known higher variance can reduce the overall variance, and that the minimum possible variance is still smaller than the variance of the asset with the smallest variance.

In reality, this scenario is actually familiar to most: think of the two assets as two dice and the portfolio return as the mean of each roll of the two dice. Actually think of 100 dice! Don't you expect that every time you roll 100 dice and calculate the mean you would get a number close to 3.5? And that the variance around the mean would indeed get smaller the larger the number of dice that you throw every time you calculate the mean?

The dice analogy works because of the expectation that all dice are fair (unbiased) and that each die rolling is independent, which implies that their they outcomes are uncorrelated. Correlation will be discussed next.

Positively correlated assets

When it comes to correlated assets, it matters whether the correlation is negative or positive. Consider first the case of the largest possible positive correlation coefficient, that is \( \rho_{x y} = 1 \). In this case, $$ \begin{aligned} \sigma^2 = \theta_x^2 \sigma^2_x + \theta_y^2 \sigma^2_y + 2 \theta_x^{} \theta_y^{} \sigma_x^{} \sigma_y^{} = (\theta_x \sigma_x + \theta_y \sigma_y)^2 = (\theta_x \sigma_x + (1 - \theta_x) \sigma_y)^2. \end{aligned} $$ If the variance of the assets is the same, that is \( \sigma_y = \sigma_x \), then $$ \begin{aligned} \sigma^2 = (\theta_x + (1 - \theta_x))^2 \sigma_x^2 = \sigma_x^2 = \sigma_y^2 \end{aligned} $$ which is the same no matter what portfolio you pick. With different variances, say \( \sigma_y = \zeta \sigma_x \), \( \zeta > 0 \), then $$ \begin{aligned} \sigma^2 = (\theta_x \sigma_x + \theta_y \sigma_y)^2 = (\theta_x + \zeta (1 - \theta_x))^2 \sigma_x^2 = (\zeta + (1 - \zeta) \theta_x)^2 \sigma_x^2. \end{aligned} $$ The minimum variance now depends on whether \( \zeta \) is smaller or larger than one. If \( \zeta > 1 \), that is if the variance of \( y \) is larger than the variance of \( x \) then $$ \begin{aligned} \sigma^2 = (\zeta + (1 - \zeta) \theta_x)^2 \sigma_x^2 \geq \sigma_x^2 \end{aligned} $$ and the portfolio with minimum variance is $$ \begin{aligned} \theta_x &= 1, & \theta_y = 0. \end{aligned} $$ Conversely, if \( 0 < \zeta < 1 \), that is if the variance of \( x \) is larger than the variance of \( y \), then $$ \begin{aligned} \sigma^2 = (\zeta + (1 - \zeta) \theta_x)^2 \sigma_x^2 \geq \zeta^2 \sigma_x^2 = \sigma_y^2 \end{aligned} $$ and the portfolio with minimum variance is $$ \begin{aligned} \theta_x &= 0, & \theta_y = 1. \end{aligned} $$

Most people would think that those results “make sense,” actually corresponding to their expectations of minimum variance. In a way, most people's intuition, in this case, is to think in terms of fully correlated assets.

At this point, a correlation that is still positive but not quite equal to one should put us somewhere between the fully positively correlated and the uncorrelated case. Indeed, that is the case, with a twist. For example, and without getting into details, if \( \sigma_y = 2 \sigma_x \), then the minimum variance is equal to $$ \begin{aligned} \sigma^2 &= \frac{4 (1 - \rho_{x y}^2)}{5 - 4 \rho_{x y}} \sigma_x^2, & \theta_x &= \frac{4 - 2 \rho_{x y}}{5 - 4 \rho_{x y}}, & \theta_y &= 1 - \theta_x, & 0 &\leq \rho_{x y} \leq \frac{1}{2}. \end{aligned} $$ But if \( 1/2 \leq \rho_{x y} \leq 1 \), then the minimum possible variance is $$ \begin{aligned} \sigma^2 &= \sigma_x^2, & \theta_x &= 1, & \theta_y &= 0, & \frac{1}{2} &\leq \rho_{x y} \leq 1. \end{aligned} $$ This is the case because beyond \( \rho_{x y} \geq 1/2 \) the minimum possible variance would require one to hold more than 100% of the first asset, which is not something that we are willing to allow in this analysis[2]. In fact, in the case of fully correlated assets, and if one is willing to go beyond a 100% in one asset, which would imply a negative holding on the other asset, then one can achieve, in principle, zero variance by letting $$ \begin{aligned} \theta_x \sigma_x &= (\theta_x - 1) \sigma_y & & \Longrightarrow & \theta_x &= \frac{1}{1 - \sigma_x/\sigma_y}. \end{aligned} $$ Note that the value of \( \theta_x \) that achieves zero variance is either larger than one or negative. In this case, simply constraining \( \theta_x \) and \( \theta_y \) from taking negative values is enough to avoid this case. We will have more to say about this in the next section.

Negatively correlated assets

We start the conversation about negatively correlated assets by again considering the case of completely negatively correlated assets, \( \rho_{x y} = -1 \), with which $$ \begin{aligned} \sigma^2 = \theta_x^2 \sigma^2_x + \theta_y^2 \sigma^2_y - 2 \theta_x^{} \theta_y^{} \sigma_x^{} \sigma_y^{} = (\theta_x \sigma_x - \theta_y \sigma_y)^2 = (\theta_x \sigma_x - (1 - \theta_x) \sigma_y)^2. \end{aligned} $$ In spite of the similarities with the formula obtained in the case of fully positively correlated assets something different seems to be at work here. Take for example the possibility of achieving zero variance, which meant in the case of positively correlated assets that one would need to hold negative portfolio positions. With negative correlations, zero variance can be achieved by setting $$ \begin{aligned} \theta_x \sigma_x &= (1 - \theta_x) \sigma_y & & \Longrightarrow & \theta_x &= \frac{1}{1 + \sigma_x/\sigma_y} \in (0, 1), \end{aligned} $$ which is a perfectly fine positive portfolio position. For example, if \( \sigma_y = \sigma_x \), then this is the equal weights portfolio $$ \begin{aligned} \theta_x &= \theta_y = \frac{1}{2}. \end{aligned} $$ The meaning of achieving zero variance in the presence of negatively correlated assets is that of hedging, which works by taking positions that are expected to move in opposite directions. If assets are identified as fully negatively correlated, all it takes is to include both assets in the portfolio, without the need to take negative positions.

Moving toward less negative correlations, we will revisit some of the same cases considered earlier. If the variance of the assets is the same, that is \( \sigma_y = \sigma_x \), then $$ \begin{aligned} \sigma^2 = (\theta_x^2 + (1 - \theta_x)^2 + 2 \rho_{x y} \theta_x (1 - \theta_x) ) \sigma_x^2 \geq \frac{1 + \rho_{xy}}{2} \sigma_x^2 \end{aligned} $$ and the portfolio that minimizes the variance is always $$ \begin{aligned} \theta_x &= \theta_y = \frac{1}{2}. \end{aligned} $$

With different variances, say \( \sigma_y = 2 \sigma_x \), then $$ \begin{aligned} \sigma^2 &= \frac{4 (1 - \rho_{xy}^2)}{5 - 4 \rho_{xy}} \sigma_x^2, & \theta_x &= \frac{4 - 2 \rho_{xy}}{5 - 4 \rho_{xy}}, & \theta_y &= 1 - \theta_x, & \theta_y &= 1 - \theta_x, & -1 &\leq \rho_{x y} \leq \frac{1}{2}, \end{aligned} $$ which is just an extension of the previously obtained formula that now covers the case of negative correlations. Interestingly, negative correlations never produce negative portfolio positions. As noted before, hedging is done implicitly by the negative correlation.

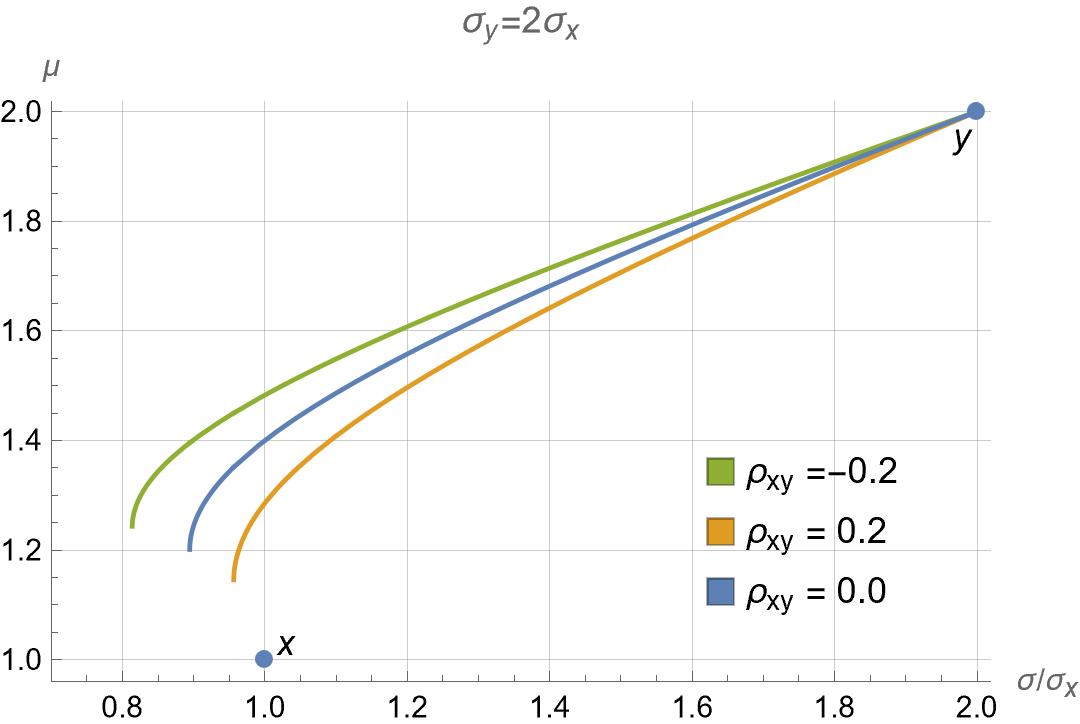
Variance

Fig.2: Variance versus return.

Variance versus return

Exclusively minimizing the variance is however rarely the main objective of portfolio optimization, after all, it is return that investors are looking for, and variance, as a measure of risk, is introduced to help guide the decision towards less risky positions. Such combination works because the variance and the return of a portfolio typically force a trade-off. We will explore those trade-offs in this section.

Take for example, the case of two uncorrelated assets with \( \sigma_y = 2 \sigma_x \) studied above. The variance of the portfolio was shown before to be equal to $$ \begin{aligned} \sigma^2 = (5 \theta_x^2 - 8 \theta_x + 4) \sigma^2_x \geq \frac{4}{5} \sigma_x^2. \end{aligned} $$ Assume now that the returns of the individual assets in the portfolio are $$ \begin{aligned} \mu_x &= 1, & \mu_y = 2, \end{aligned} $$ which is the typical case in which larger returns come with larger risk (variance), so that the portfolio return is $$ \begin{aligned} \mu &= \theta_x \, \mu_x + \theta_y \, \mu_y = \theta_x + 2 (1 - \theta_x) = 2 - \theta_x. \end{aligned} $$ In this simple case of only two assets, the position $$ \begin{aligned} \theta_x = 2 - \mu \end{aligned} $$ is a straightforward function of the portfolio return. Moreover, any return \( \mu \) between \( \mu_x = 1 \) and \( \mu_y = 2 \) leads to a positive position, for which we can calculate the corresponding variance. The result is the blue curve in Fig. 2, in which the standard deviation of the portfolio is in the x-axis and the return is in the y-axis. This somewhat peculiar way of plotting return versus variance is the norm in portfolio analysis. A couple of comments are in order:

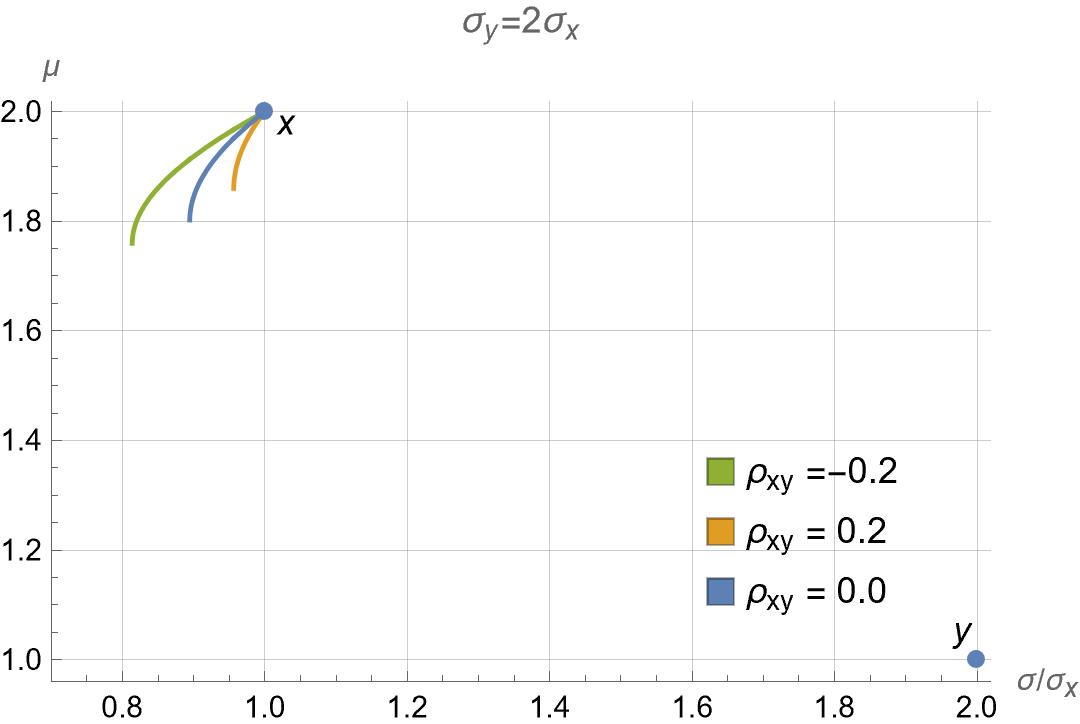
Variance

Fig.3: Variance versus return.

A similar picture can be drawn for the same variance scenario but the unusual returns $$ \begin{aligned} \mu_x &= 2, & \mu_y = 1. \end{aligned} $$ Note that in this case the asset with the largest return is the one with the smallest variance, so one would expect that an investor seeking to maximize the portfolio return would simply pick 100% of the asset \( x \). While that is indeed the case, the plots in Fig. 3 show that, perhaps contrary to intuition, it is possible to further reduce the variance by sacrificing a small portion of the return and holding some amount of the asset \( y \) that has larger variance and smaller return. The amount of variance reduction possible depends on the correlation of the assets. The minimum possible variance gets smaller as the assets' correlation gets smaller.

The Covariance of Many Assets

The above analysis can be extended to an arbitrary number of assets. In a portfolio with many assets, the expected return and variance of the portfolio is $$ \mu = \theta_1 \, \mu_1 + \theta_2 \, \mu_2 + \cdots + \theta_n \, \mu_n = \sum_{i= 1}^n \theta_i \, \mu_i, $$ and the variance is $$ \sigma^2 = \sum_{i = 1}^n \sum_{j = 1}^n c_{i, j} \,\theta_i \, \theta_j $$ in which $$ \begin{aligned} \mu_{i} &= E \{ r_i \}, & c_{i,j} &= E \{ (r_i - \mu_i) (r_j - \mu_j) \}. \end{aligned} $$ In this notation, \( c_{i, j} \) is the correlation between assets \( i \) and \( j \) and \( c_{i, i} \) is the variance of the \( i \)th asset. It is convenient to assemble the coefficients of the above calculation into the vectors and matrix $$ \begin{aligned} r &= \begin{pmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_n \end{pmatrix}, & \theta &= \begin{pmatrix} \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{pmatrix}, & C = \begin{bmatrix} c_{1,1} & c_{1,2} & \cdots & c_{1,n} \\ c_{2,1} & c_{2,2} & \cdots & c_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{n,1} & c_{n,2} & \cdots & c_{n,n} \end{bmatrix}. \end{aligned} $$ The matrix \( C \) is known as the covariance matrix. Note that the covariance matrix is symmetric because \( c_{i ,j} = c_{j, i} \). Using this notation, the return and the variance of the portfolio become simply $$ \begin{aligned} \mu &= r^T \theta, & \sigma^2 &= \theta^T C \theta. \end{aligned} $$ In the case of two assets, the covariance matrix is the 2-by-2 matrix $$ \tag{1} \label{eq:cov2} C = \begin{bmatrix} \sigma_x^2 & \rho_{x, y} \sigma_x \sigma_y \\ \rho_{x, y} \sigma_x \sigma_y & \sigma_y^2 \end{bmatrix}. $$

Some properties of the covariance matrix are only revealed after applying some transformations. One such useful transformation is the factorization $$ \begin{aligned} C &= V D V^T, & V^T V &= I, & D &= \begin{bmatrix} d_1 & 0 & \cdots & 0 \\ 0 & d_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & d_n \\ \end{bmatrix}, & d_i &\geq 0, \end{aligned} $$ in which \( D \) is a diagonal matrix. The particulars of the formulas are not as important as the shape of the arrays. The \( d_i \)'s are the components of the variance, and the \( i \)th column of the matrix \( V \) represents a combination of the original assets that is uncorrelated with the combinations produced by the other columns of \( V \) and has variance \( d_i \).

In the 2-by-2 case, diagonalization means that $$ \begin{aligned} C &= \begin{bmatrix} v_{1,1} & v_{1,2} \\ v_{2,1} & v_{2,2} \end{bmatrix} \begin{bmatrix} d_1 & 0 \\ 0 & d_2 \end{bmatrix} \begin{bmatrix} v_{1,1} & v_{2,1} \\ v_{1,2} & v_{2,2} \end{bmatrix}, & d_1 &= \frac{1}{2} \left ( \sigma_x^2 + \sigma_y^2 + \sqrt{\Delta} \right ), & d_2 &= \frac{1}{2} \left ( \sigma_x^2 + \sigma_y^2 - \sqrt{\Delta} \right ), \end{aligned} $$ in which $$ \begin{aligned} \Delta &= \sigma_x^4+2 \sigma_x^2 \left(2 \rho_{xy}^2-1\right) \sigma_y^2 + \sigma_y^4. \end{aligned} $$ If \( \rho_{x,y} = 0 \) and \( \sigma_x \geq \sigma_y \) then \( d_1 = \sigma_x^2 \) and \( d_2 = \sigma_y^2 \), as expected, since the original assets were already uncorrelated. However, if \( \rho_{x,y} = 1 \) or \( \rho_{x,y} = -1 \) then \( d_1 = \sigma_x^2 + \sigma_y^2 \) and \( d_2 = 0 \). Note that the non-zero variance component \( d_1 \) is the same regardless if the correlation is positive or negative.

Take for a concrete example the case \( \sigma_y = 2 \sigma_x \) discussed before. When \( \rho_{xy} = \pm 1 \), then $$ \begin{aligned} C &= \sigma_x^2 \begin{bmatrix} 1 & \pm 2 \\ \pm 2 & 4 \end{bmatrix}, & V &= \frac{1}{\sqrt{5}} \begin{bmatrix} \pm 1 & \mp 2 \\ 2 & 1 \end{bmatrix}, & D &= \begin{bmatrix} 5 \, \sigma_x^2 & 0 \\ 0 & 0 \end{bmatrix}. \end{aligned} $$ Note that it is the sign of the entries in the coefficient array \( V \) that identifies the sign of the correlation. In either case, as mentioned before, it is possible to find a portfolio that achieves zero variance. Because the columns of \( V \) represent uncorrelated combinations of assets, if we set $$ \theta = \frac{1}{1 \mp 2} \begin{pmatrix} \mp 2 \\ 1 \end{pmatrix} $$ as a multiple of the second column of \( V \), then $$ \sigma^2 = \theta^T C \theta = 0. $$ As seen before, in the case of positive correlation the zero variance portfolio can only be realized with short sales, while in the case of negative correlation it is a portfolio with non-negative positions. Finally, because of the zero in \( d_2 \), the covariance matrix can be described more compactly as $$ \begin{aligned} C &= \sigma_x^2 \begin{bmatrix} \pm 1 \\ 2 \end{bmatrix} \begin{bmatrix} \pm 1 & 2 \end{bmatrix}. \end{aligned} $$

Similar conclusions carry over to the case of multiple assets:

Before moving on, we consider a last example to illustrate that it is not always straightforward to generalize our intuitive understanding of correlation from two to multiple assets. For example, consider the following matrix as a possible covariance matrix: $$ \begin{aligned} C &= \begin{bmatrix} 1 & 0 & \rho \\ 0 & 1 & \rho \\ \rho & \rho & 1 \end{bmatrix}. \end{aligned} $$ One might think it is possible for \( \rho \) to be equal to one, which, according to our 2-by-2 notion of correlation, would seem to imply that the third asset is fully correlated with the first and second assets. It turns out that this is impossible[4,5], and one can show that \( \rho \) must be such that \( |\rho| \leq \sqrt{2}/2 \).

Interestingly enough, when \( \rho = \sqrt{2}/2 \) then $$ \begin{aligned} C &= \begin{bmatrix} \rho & \rho & 0 \\ \rho & -\rho & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} \rho & \rho & 0 \\ \rho & -\rho & 0 \\ 0 & 0 & 1 \end{bmatrix}^T \end{aligned} $$ which reveals that the transformed variables $$ \begin{aligned} y_1 &= \rho \, (x_1 + x_2), & y_2 &= \rho \, (x_1 - x_2), & y_3 &= x_3, \end{aligned} $$ are such that \( y_1 \) is not correlated with \( y_2 \) nor \( y_3 \) and that \( y_2 \) and \( y_3 \) are fully positively correlated. In order to “discover” these “hidden” correlations it was necessary to look beyond the individual assets, that is look into possible combinations of assets. The discovery of such not very obvious relationships among the assets is one of the many aspects that makes portfolio optimization a useful tool for investors.

Estimating the Covariance Matrix

Covariance provides a solid foundation from which to start exploring and, hopefully, also exploiting the correlation of multiple assets. However, estimating a complete covariance matrix for a portfolio with a large number of assets is not an easy task. There are several practical obstacles that make the resulting estimates not very accurate. One is the demand for a large number of samples. Perhaps the most straightforward covariance estimate is the following generalization of the univariate sample variance formula shown at the beginning of this note: $$ \begin{aligned} \hat{\mu} &= \frac{1}{N} \sum_{k = 1}^N x_k, & \hat{C} &= \frac{1}{N-1} \sum_{k = 1}^N (x_k - \hat{\mu}) (x_k - \hat{\mu})^T, \end{aligned} $$ in which the \( x_k \)'s are now \( n \)-dimensional vectors instead of scalar samples. One immediate difficulty is the fact that if \( N < n \), then \( \hat{C} \) will be such that at least \( N - n \) variance components are exactly zero. In order to avoid zero principal components, one must therefore obtain at least \( N \geq n \) samples. In a portfolio with thousands or even as little as hundreds of assets, this may not be possible or, when possible, might span a too large time interval as to render the exercise irrelevant. In practice, one may end up employing approximate regularization techniques [1], especially if the covariance matrix is to be inverted. The literature on the subject is extensive, and no single method fits all applications. See, for instance, [2], for a more in-depth discussion. For finance applications, the best methods seem to be the ones based on factor models, which we discuss next.

Factor Models

Start by considering the seemingly unrelated problem of comparing the return of an asset to the return of the market. Putting aside the perennial debate of what is it that constitute the market, take a portfolio with enough diversification or a large basket of assets, such as the S&P 500, as a proxy for the market. Then posit that the return of a select asset, \( r_x \), and the return of the market proxy, \( v \), are related by $$ \tag{2} \label{eq:model} r_x - \mu_x = \beta \, (v - \mu_v) + \epsilon $$ in which \( \epsilon \) is a zero-mean random variable with variance \( \sigma_\epsilon^2 \) that represents model errors. If we assume that the model errors \( \epsilon \) are uncorrelated with the market, then the covariance matrix of the asset and the return is equal to $$ \begin{aligned} C &= \begin{bmatrix} \sigma_x^2 & \beta \, \sigma_v^2 \\ \beta \, \sigma_v^2 & \sigma_v^2 \end{bmatrix}, & \sigma_x^2 &= \sigma_\epsilon^2 + \beta^2 \sigma_v^2. \end{aligned} $$ Comparing this covariance matrix with the matrix in \( \eqref{eq:cov2} \) with \( \sigma_v \) in place of \( \sigma_y \), we have that $$ \beta = \frac{\rho_{x v} \, \sigma_x}{\sigma_v}. $$ This means that knowledge of the coefficient \( \beta \) is equivalent to knowledge of the correlation between the asset and the market. This is akin to the classic CAPM (Capital Asset Pricing Model)[3], which relates the expected return of an asset with the expected rate of return of the market.

Conversely, if \( \beta \) and the model errors \( \epsilon \) are calculated, for example after fitting a model of the form \( \eqref{eq:model} \), then $$ \sigma_x^2 = \sigma_\epsilon^2 + \beta^2 \sigma_v^2. $$ is the covariance of the asset that we are looking for. In the case of multiple assets we can use this framework to construct the covariance matrix of the entire portfolio. Indeed, if we let \( r_x \), \( \epsilon \), and \( \beta \) be vectors in \( \eqref{eq:model} \), then $$ C = \begin{bmatrix} C_x & \beta \, \sigma_v^2 \\ \beta^T \sigma_v^2 & \sigma_v^2 \end{bmatrix} $$ in which the matrix $$ C_x = \Sigma_x + \sigma_v^2 \, \beta^{} \beta^T $$ is the portfolio covariance matrix. The “unsystematic” part of the covariance, that is the matrix \( \Sigma_x \), is often approximated as a diagonal matrix which can be estimated, for example, as the sample variances of the residues in the model. For example, in the case of two assets the factor model $$ \begin{aligned} \begin{pmatrix} r_1 - \hat{\mu}_{1} \\ r_2 - \hat{\mu}_{2} \end{pmatrix} &= \begin{pmatrix} \beta_{1} \\ \beta_{2} \end{pmatrix} (v - \hat{\mu}_{v}) + \begin{pmatrix} \epsilon_{1} \\ \epsilon_{2} \end{pmatrix}, \end{aligned} $$ produces the 2-by-2 covariance matrix $$ C_x = \begin{bmatrix} \sigma_{\epsilon_1}^2 + \sigma_v^2 \, \beta_1^2 & \sigma_v^2 \, \beta_1 \beta_2 \\ \sigma_v^2 \, \beta_1 \beta_2 & \sigma_{\epsilon_2}^2 + \sigma_v^2 \, \beta_2^2. \end{bmatrix}. $$ Note how it is the product of the coefficients \( \beta_1 \beta_2 \) encode the correlation between the two assets. In fact, part of the magic of factor models is the ability to infer the correlation between assets without directly comparing them. Instead, the covariance is obtained by assessing how each asset is related with the market.

Factor models can be generalized not only to multiple assets, but also to multiple market assets, which are referred to as the model factors. Besides assets, one can use indices, indicators, or other fundamental variables as factors.

Given a set of market assets, one estimates a linear relationship between the return of \( n \) assets and \( m \) factors of the form $$ \begin{aligned} r_1 - \hat{\mu}_{1} &= \beta_{1,1} \, (v_1 - \hat{\mu}_{v_1}) + \beta_{1,2} \, (v_2 - \hat{\mu}_{v_2}) + \cdots + \beta_{1,m} \, (v_m - \hat{\mu}_{v_m}) + \epsilon_1, \\ r_2 - \hat{\mu}_{2} &= \beta_{2,1} \, (v_1 - \hat{\mu}_{v_1}) + \beta_{2,2} \, (v_2 - \hat{\mu}_{v_2}) + \cdots + \beta_{2,m} \, (v_m - \hat{\mu}_{v_m}) + \epsilon_2, \\ \vdots \qquad & \qquad \vdots \\ r_n - \hat{\mu}_{n} &= \beta_{n,1} \, (v_1 - \hat{\mu}_{v_1}) + \beta_{n,2} \, (v_2 - \hat{\mu}_{v_2}) + \cdots + \beta_{n,m} \, (v_m - \hat{\mu}_{v_m}) + \epsilon_n, \end{aligned} $$ in which the \( \epsilon_i \)'s represent modeling errors and the \( \hat{\mu} \)'s are estimates of the mean return of the assets and the factors. The underlying model is the same as \( \eqref{eq:model} \) in which \( v \) is now a vector and \( \beta \) a rectangular array. The portfolio covariance matrix is then $$ \begin{aligned} C_x &= \Sigma_x + \beta \, C_v \, \beta^T, \end{aligned} $$ which can be calculated after estimating \( \beta \), \( \Sigma_x \), and \( C_v \) from historical data. Typically, the number of factors are kept small, from one to tens of assets or indicators, while the number of portfolio assets can be in the thousands. In this way, we guarantee that the entries in the market correlation matrix \( C_v \) are accurately estimated.

When estimating the parameters of a factor model it is important to be careful with the nature of the returns employed in the estimates. In the Models API we apply the same methodology discussed earlier in case study to anchor the returns to the present date instead of simply averaging incremental daily returns, which provides a much more sound metric for investors. As discussed in detail in the case study, returns and variances of exponential return models are better estimated using log-prices. A variant of these ideas is used also to estimate the covariance of the market. The resulting factor models has a high degree of interpretability and can be validated against the log-price series.

Mauricio de Oliveira

References

  1. O. Ledoit and M. Wolf, “A well-conditioned estimator for large-dimensional covariance matrices,” Journal of Multivariate Analysis 88 (2): 365–411, 2004.
  2. Jianqing Fan, Yuan Liao, Han Liu, “An overview of the estimation of large covariance and precision matrices,” The Econometrics Journal 19 (1): C1–C32, 2016
  3. Edwin J. Elton and Martin J. Gruber, Modern Portfolio Theory and Investment Analysis. Fifth Edition, John Wiley and Sons, 1995.

Notes

  1. We limit our attention to the case of non-negative portfolio positions.
  2. This could be possible if one holds a negative position on the second asset, that is if we allow “short-sales.”
  3. The covariance matrix is not full rank in this case.
  4. This matrix is not positive semi-definite, hence it cannot be a covariance matrix.
  5. For those seeking for a more intuitive “explanation,” if the 2-by-2 reasoning would apply verbatim, how could one asset be fully correlated with two other assets that are themselves uncorrelated?

Copyright © 2009, 2024 VICBee Consulting